In this section we are going to make a comparison between the three theoretical cycles of thermal motors. We will compare in the Otto cycle, with the Diesel cycle and with the Sabathé mixed cycle.
To compare the mentioned cycles, it is necessary to take as a reference some of the factors whose value depends on the shape and surface of the engine, such as: the compression ratio, the maximum pressure, the amount of heat supplied, the heat subtracted and the work Useful.
The following figure shows the curves of the ideal thermal efficiency variations by varying the compression ratio for the three cycles: Otto, Diesel and Sabathé. For the Diesel and Sabathé cycles, a constant pressure combustion ratio equal to 2 has been chosen.
As seen in the figure, the thermal yields of the theoretical cycles increase as the compression ratio increases. For a given relationship of this type, the Otto cycle gives higher performance, while the Diesel cycle results in lower performance. It should be considered, however, that for Diesel engines, the compression ratio varies between 14 and 22. On the other hand, for spark ignition engines the compression ratio generally does not exceed the value of 10, in order to avoid detonation
Therefore, the diesel engine has a higher thermal efficiency than the Otto engine .
Comparison matching the compression ratio and the heat supplied
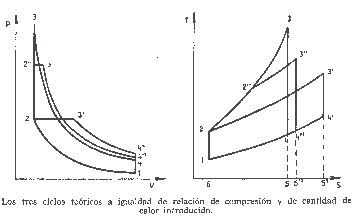In the second figure, the three theoretical cycles are compared in PV coordinates (pressure - volume) and TS (temperature - entropy). In this study, the compression ratio and the amount of heat supplied are equalized. All cycles begin in the same condition 1 and have the same adiabatic compression of 1 to 2.
In order that the amount of heat supplied is the same in all three cases, the surfaces in TS coordinates, 2 '' 3 '' 5 '' 6 2 2 '', 2 3 '5' 6 2 and 2 3 5 6 2 must be the same.
Taking into account that heat is subtracted at the same specific volume, according to the transformation line between states 4 and 1, the amount of heat subtracted is represented, for each cycle, by the surface itself below line 4-1 in the TS diagram. Since the heat supplied is the same for each cycle, it turns out that the theoretical cycle with the highest thermal efficiency is the one in which less heat is subtracted. In this case, it is the Otto cycle, for which the surface representing the amount of heat subtracted is defined in TS coordinates by points 4 5 6 1 4.
It should be noted that the maximum pressure and temperature in the Otto cycle are much higher than in the other two cycles. Although this comparison is purely theoretical, it serves to demonstrate that the cycle that provides the greatest expansion of the fluid after the heat introduction phase is the highest performance.
We will indicate for the various cycles with r E the relationship between the volumes at the end of the expansion stroke and at the end of the heat introduction phase.
For the Otto cycle it turns out:
while for the Diesel cycle we have:
Conclusions of the comparison of the theoretical cycles
We can, therefore, admit the expansion ratio thus defined as the index of cycle performance.
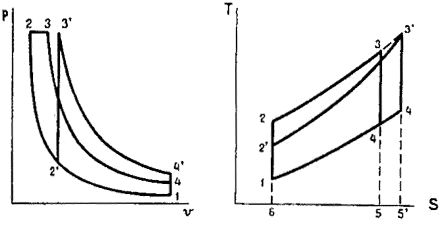In the figure on the left, the comparison between Otto, Diesel theoretical cycles is made at equal pressure and maximum amount of heat supplied. Under these conditions the surfaces 2 3 5 6 2 and 2 '3' 5 '6' 2 'must be equal.
The Diesel cycle is one in which the least amount of heat is subtracted, and since the surface that represents the subtracted heat is 4 5 6 1 4, it follows, therefore, that under these conditions the Diesel cycle is the one with the highest performance.
Also in this case it is evident that the cycle that allows the greatest expansion of the fluid after combustion is the one with the highest thermal efficiency.