The Sabathé cycle is a thermodynamic cycle applied to internal combustion engines in which combustion occurs in two phases: one at constant pressure and one at constant volume. Due to this combination, it is also known as a mixed cycle, dual combustion cycle or limited pressure cycle. This model better reflects the real working conditions of diesel engines compared to ideal Otto and Diesel cycles.
The Sabathé cycle, also called the mixed Sabathé cycle, is called by different names depending on its approach and characteristics. It is known as a dual combustion cycle because it combines two combustion processes: one at constant volume and one at constant pressure. It is also called a pressure-limited cycle, since in the second combustion phase the pressure does not continue to increase indefinitely. The names Trinkler cycle and Seiliger cycle come from the engineers who studied and described their principles.
Differences with Otto and Diesel cycles
In practice, diesel engines do not operate exactly under the ideal Diesel cycle, since combustion does not occur completely at constant pressure. In most engines, especially medium and high speed ones, combustion resembles a combination of the Otto and Diesel cycles, resulting in the Sabathé cycle.
At equal compression ratio:
-
If most of the heat is introduced at constant volume, the efficiency approaches that of the Otto cycle.
-
If the heat is introduced mostly at constant pressure, the performance is similar to that of the Diesel cycle.
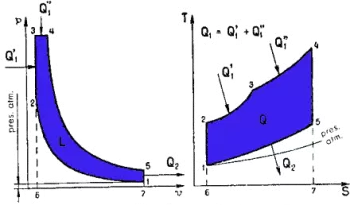
Description and calculation of the Sabathé mixed cycle
The cycle consists of the following phases:
- Adiabatic compression (1-2) : Air is compressed without heat exchange.
- Constant volume combustion (2-3) : Part of the heat (Q1') is introduced, raising the pressure without modifying the volume.
- Constant pressure combustion (3-4) : The rest of the heat (Q1'') is introduced, increasing the volume without modifying the pressure.
- Adiabatic expansion (4-5) : The gas expands without heat exchange, performing mechanical work.
- Constant volume heat extraction (5-1) : Residual heat (Q2) is extracted by reducing pressure and temperature.
In this cycle, the adiabatic compression phase 1-2 is followed by a constant volume combustion phase 2-3. During this combustion phase, the amount of heat Q1' is introduced, followed by, as in the Diesel cycle, a constant pressure combustion phase 3-4, during which the amount of heat Q1'' is introduced.
Then follow two successive phases, namely: one of adiabatic expansion 4-5, and another of subtraction, at constant volume 5-1, of the quantity of heat Q2.
Therefore, the total amount of heat introduced equals:
Q1=Q1’+Q1’’
Recalling what has been said, regarding the Otto and Diesel cycles, we can write:
Q 1 '=C v (T 3 -T 2 )
Q1’’= Cp (T4-T3)
Q 2 = C v (T 5 -T 1 )
Thus, the ideal thermal efficiency of the theoretical Sabathé cycle equals:
h e = (heat supplied – heat subtracted)/ heat supplied
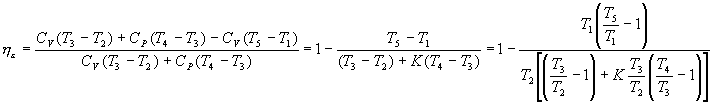
For transformation 2-3 of constant volume combustion we have:
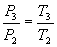
And for transformation 3-4 of constant pressure combustion:
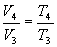
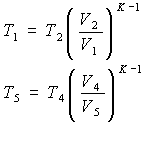
For adiabatic transformations 1-2 of compression and 4-5 of expansion we will use, respectively, the formulas
from which we obtain:
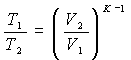

and being V 3 = V 2 ; V 5 = V 1
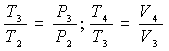
can be written:
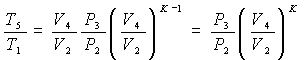
Substituting these expressions into those of ideal thermal efficiency, we obtain:
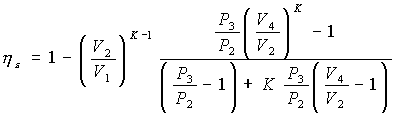
Let's start with the relationship between the pressure P3 at the end and the pressure P2 at the beginning of the constant volume combustion phase – which we will call the “constant volume combustion ratio” – and remembering that:
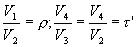
the final expression of ideal thermal efficiency of the theoretical Sabathé cycle is obtained :
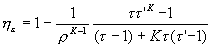
Conclusions on the performance of the Sabathé cycle
For the same compression ratio r, the efficiency of the mixed cycle is intermediate between that of the Otto cycle and that of the Diesel cycle. If the heat supplied at constant volume is increased, i.e. between points 2 and 3, and the heat supplied at constant pressure is reduced between points 3 and 4, the thermal efficiency approaches that of the Otto cycle. If, on the other hand, the heat supplied at constant volume is reduced and the corresponding heat at constant pressure is increased, the efficiency of the mixed cycle approaches that of the Diesel cycle.