The theoretical Otto cycle is the ideal Otto engine cycle. The Otto engine is also known as a positive ignition engine because the fuel is ignited through a spark caused by a spark plug. It is also known as a gasoline engine because of the type of fuel it uses.
One way to study the performance of this engine is by analyzing its theoretical cycle. The theoretical cycle is an approximation to the real cycle with many simplifications. In practice, so many variables appear that affect engine performance that calculating the actual cycle is practically impossible. Anyway the theoretical cico Otto is a good approximation to the real cycle.
What is the 4-stroke Otto cycle like?
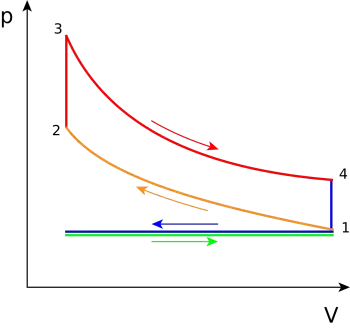
The following diagrams represent the Otto cycle in a 4-stroke engine in both PV and TS coordinates.
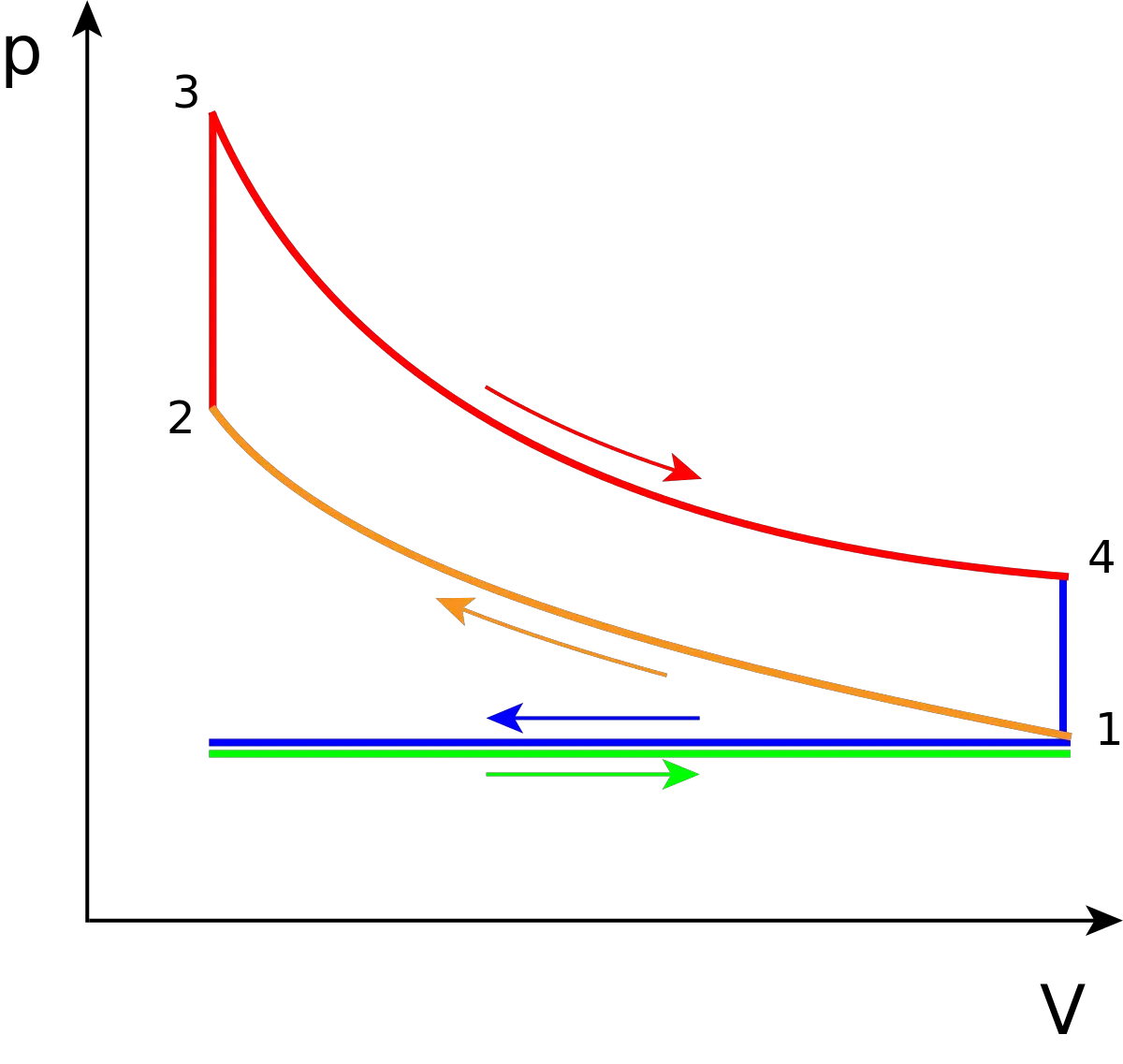
The thermodynamic transformations that take place during the Otto cycle are:
- 1-2. Adiabatic and isentropic transformation (without heat exchange with the outside). Compression of the active fluid and corresponding to the work L 1 performed by the piston.
- 2-3. Transformation at constant volume. Instantaneous introduction of supplied heat Q 1 .
- 3-4. Adiabatic transformation. Expansion at constant pressure and corresponding work L 2 produced by the active fluid.
- 4-1. Transformation at constant volume. Instantaneous heat removal Q 2 .
In reality, in the 4-stroke engine, heat subtraction occurs during the 1-0 exhaust stroke, and the fluid is introduced into the engine in the 0-1 suction stroke, which is graphically represented in the diagram PV by a horizontal line, while in the TS diagram it is not possible to represent it. The effects of both processes cancel each other out, without gain or loss of work, which is why the suction and exhaust strokes are not usually considered in ideal diagrams in PV coordinates, and the Otto cycle is represented as a closed cycle, in the which the active fluid returns to its initial state when the heat expulsion phase 4-1 comes to an end.
What is the 2-stroke Otto cycle like?
The Otto cycle changes slightly in a 2-stroke engine compared to the 4-stroke engine.
First half - Compression amdision
When the reciprocating engine piston reaches PMI (Lower Dead Center) it begins to travel to TDC (Top Dead Center). During the stroke, the piston creates a pressure difference that draws the air-gasoline mixture through the intake port towards the pre-compression crankcase. Fuel enters in gaseous form.
When the piston plugs the port, the mixture stops entering. During the remainder of the downward stroke, the piston is compressed by the mixture in the lower crankcase, until the transfer port that communicates it with the compression chamber is uncovered. By communicating with the compression chamber, the fresh, pre-compressed mixture helps to expel the burned gases from the exhaust.
When the piston starts to rise, the transfer port remains open a part of the stroke and the crankcase does not take in fresh air, but part of the gases return, losing pumping efficiency.At high revolutions, the inertia of the mass of the gases is used to minimize this effect. It is what is called renewal of the load.
Second time. Expansion and exhaust of gases
Once the piston of the heat engine has reached TDC and the mixture of air and gasoline is compressed, it is ignited by a spark between the two electrodes of the spark plug. With ignition the fuel releases energy and reaches high pressures and temperatures in the cylinder. The piston travels downward, doing work until the exhaust port is exposed. Being at high pressures, the burned gases come out through this hole.
Characteristics of the 2-stroke Otto cycle
The performance of this engine is lower compared to the 4-stroke engine, as it has a lower volumetric efficiency and the exhaust is less efficient. The 2-stroke cycles are more polluting. At the power level, the 2-stroke Otto cycle offers a higher torque in the unit of time for the same displacement. This difference in torque is due to the fact that the 2-stroke engine explodes with every revolution, while the 4-stroke engine explodes every 2 revolutions, and has more moving parts.
This type of engine is used mainly in small displacement engines (mopeds, brush cutters, hedge trimmers, chainsaws, etc.), since it is cheaper and easier to build, and its high emission of pollutants is very low in absolute value.
What is the performance of the Otto cycle?
Since the heat Q1 is introduced at constant volume, the L 2-3 work done during this transformation is zero, and the equation for the conservation of energy of the fluid without flow becomes:
As it is an ideal cycle and, therefore, the working fluid is a perfect gas, the variation of the internal energy during its transformation to constant volume is equal to:
Where does it come from:
Similarly, as heat Q 2 is also subtracted at constant volume, and under such conditions that L 4-1 = 0, we can write:
and because the fluid is a perfect gas:
Therefore, the ideal thermal performance for the theoretical Otto cycle is:
h e = (heat supplied - heat subtracted) / heat supplied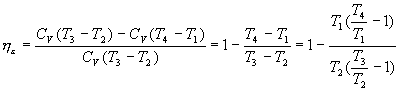
For the adiabatic transformations of compression 1-2 and expansion 3-4 we obtain, respectively:
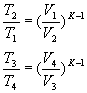
and since it is V 1 = V 4 and V 2 = V 3 , we can write:
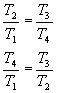
Introducing this relationship in the expression of the performance h e (as well as the one that exists between the temperatures T 1 and T 2 of phase 1-2 of adiabatic compression), it results:
Indicating with 
the relationship between the respective volumes V 1 and V 2 of the beginning and end of the compression stroke –which we will call “volumetric compression ratio” -, the final expression of the ideal thermal performance of the Otto cycle is obtained .
The thermal efficiency of the Otto cycle is, therefore, a function of the compression ratio and exponent k, the ratio of the specific heats of the working fluid. Increasing , increase h e ; increasing the values of the specific heats, k decreases and, consequently, also the thermal efficiency h e . Therefore, the ideal cycle, for which k = 1.4, has a higher thermal performance than the air cycle, given the case that, for this, k has a lower average value, due to varying the specific heats with temperature.